
이 문제는 규칙적인 신체활동과 운동이 우리 몸에 주는 생리학적 이점을 물어보는 문제야.
ACSM 11판에서도 “운동의 만성적 효과(Chronic Adaptations to Exercise)” 파트에서 명확하게 정리되어 있어.
✅ 문제
규칙적인 신체활동과 운동의 이점으로만 고른 것은?
<보기>
① 절대적 최대하 강도에서 분당호흡량과 심근산소소비량 증가
② 안정 시 수축기 혈압과 이완기 혈압 감소
③ 최대산소섭취량 증가와 안정 시 심박수 감소
④ 인슐린 감수성과 포도당 내성 감소
✅ 정답: ②번 ㄴ,ㄷ
📘 ACSM 11판 기준: 운동의 이점
🟢 운동이 우리 몸에 주는 대표적 ‘긍정적’ 효과들
| 신체계통 | 운동의 이점 |
| ❤️ 심혈관계 | ▪ 안정시 심박수(HR) 감소 → 심박출량↑ ▪ 안정시 수축기/이완기 혈압 감소 ▪ 혈관 탄성 증가 |
| 🫁 호흡계 | ▪ 폐활량, 분당환기량 증가 ▪ 운동 중 호흡 효율 증가 |
| 🧠 신경계 | ▪ 자율신경 균형 개선 → 부교감 활성↑ |
| 🦴 대사계 | ▪ 인슐린 감수성 증가 ▪ 포도당 내성 개선 ▪ 복부지방 감소 |
| 🏃 운동능력 | ▪ 최대산소섭취량(VO₂max) 증가 ▪ 운동 내성 증가 |
🔍 보기 분석
| 보기 | 설명 | 판별 | 이유 |
| ➀ | 최대하 강도에서 분당호흡량 & 심근산소소비량 증가 | ❌ 단점 아님, 일시적 증가 | 훈련 후엔 같은 운동 강도에 더 적은 산소 소비 |
| ➁ | 안정 시 혈압 감소 | ✅ | 대표적 만성 효과 |
| ➂ | VO₂max 증가 & 안정시 HR 감소 | ✅ | 심장 효율성 증가 |
| ➃ | 인슐린 감수성과 포도당 내성 감소 | ❌ | 감수성은 증가, 내성은 감소가 정답! → 문장 반대로 되어 있음 |
🟡 주의 포인트
- 인슐린 감수성 ↑ (=좋음)
- 포도당 내성 ↓ (=좋음 → 혈당을 잘 조절함)
👉 보기 ➃는 헷갈리게 만든 함정 문장이다냥!
🐾 한줄 요약
규칙적인 운동은 심장 덜 뛰고, 혈압 낮추고,
산소 더 잘 쓰고, 혈당도 안정시켜주는 착한 고양이 같은 존재다냥 🐱💓

이 문제는 ‘국민체력100’ 노인 체력평가 항목 중에서 정확한 측정 목적과 방법이 연결된 경우만 고르라는 문제인데,
보기 중에서 ➁(협응력), ➃(근지구력)는 틀린 설명이라서
✅ 정답은 ③번: ➀ 유연성, ➁ 보행 및 동적평형성이 맞다냥!
📘 국민체력100 노인 체력 측정 항목 요약
| 측정 요쇼 | 검사 항목 | 측정 목적/설명 |
| 🟢 ➀ 유연성 | 의자에 앉았다 일어서기 | 상지 유연성 & 어깨 가동성 |
| 🟢 ➁ 보행/평형성 | 3m 돌아오기 | 하체 기능 + 이동능력 + 속도 |
| 🔴 ➂ 협응력 | 8자 보행 검사 ❌ → 정확히는 평형성/기능성 이동능력 평가 | |
| 🔴 ➃ 근지구력 | 2분 제자리 걷기 ❌ → 심폐지구력(심폐기능) 항목에 해당됨 |
🔍 선지별 분석
| 보기 | 측정요소 | 설명 | 판별 |
| ➀ | 유연성 | 의자에 앉았다 일어서기 & 팔 교차 움직임 | ✅ |
| ➁ | 보행/동적 평형성 | 의자→3m→다시 돌아오는 시간 측정 | ✅ |
| ➂ | 협응력 | 8자 보행은 실제로는 균형+이동능력 | ❌ |
| ➃ | 근지구력 | 2분 제자리 걷기 = 심폐지구력 평가 | ❌ |
🧠 꿀팁: 국민체력100 노인 평가 항목 정리
| 체력 요소 | 검사 항목 | 비고 |
| 유연성 | 의자에 앉았다 팔 교차 | 상지 유연성 |
| 하지근력 | 30초 의자 일어서기 | 근력 |
| 보행능력 | 3m 왕복 걷기 | 이동속도 |
| 균형능력 | 일발서기 | 정적 균형 |
| 심폐지구력 | 2분 제자리 걷기 | 무릎 높이 기준 |
| 협응력 | 팔/다리 움직임 맞추기 (일부 프로그램에서 사용) | 비공식 항목인 경우도 있음 |
🟣 기억 포인트
노인 체력검사 항목은 "안전+기능" 중심!
고난이도 테스트보단 **일상생활 독립성(ADL)**과 관련된 능력 측정이 핵심이다냥 😺

✅ 문제 요약
<보기>
- "심박수와 수축기 혈압을 곱한 값이다."
- "관상동맥 혈류 공급과 수요의 문제로 발생되는 심근허혈 증상과 관련이 있다."
👉 정답: ③ 심근산소요구량(RPP)
📘 개념 정리
🔴 RPP (Rate Pressure Product = 심근산소요구량)
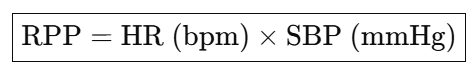
- HR: 심박수
- SBP: 수축기 혈압
- 단위는 없지만 → 심장의 부담, 산소 소비 요구를 간접적으로 나타냄
- 👉 RPP가 높다 = 심장이 많이 일하고 있다 = 산소 많이 필요하다
RPP와 관련 있는 임상적 내용:
- 협심증(Angina) 기준점으로 사용
- 운동 중 가슴 통증이 시작되는 RPP를 기준으로 운동강도 설정함
🔵 선지 헷갈림 정리
| 보기 | 용어 | 의미 | 판별 |
| ① VO₂max | 최대 산소섭취량 | 전신의 최대 산소 이용 능력 | ❌ |
| ② Cardiac Output | 심박출량 = HR × SV | 1분간 심장이 내보내는 혈액량 | ❌ |
| ③ RPP | HR × SBP → 심근산소요구량 | 정답! | ✅ |
| ④ Palpitations | 심계항진 = 가슴이 두근거림 | 자각 증상, 병리적 용어 | ❌ |
🧠 꿀팁 비유
RPP는 "심장이 지금 얼마나 힘든지 보여주는 체력 게이지"다냥
마치 자동차의 RPM처럼, 너무 올라가면 엔진(심장)이 터질 수도 있음! 🏎️💥
🐾 보너스: RPP 수치로 심장 부담 간단 구분
| RPP 수치 | 심장 부담 정도 |
| < 10,000 | 낮은 부담 |
| 10,000 ~ 20,000 | 중간 |
| > 20,000 | 높은 부담, 협심증 주의 |
다음부턴 VO₂max는 "전신의 최대 퍼포먼스 지표"
RPP는 "심장이 얼마나 힘든가를 보여주는 지표"
👉 이렇게 구분해서 생각하자쟝 😼
🟢 정상적인 최고 RPP 범위
| 구분 | 수치 | 의미 |
| 🔹 정상인의 최대 RPP | 25,000 ~ 40,000 mmHg·beats/min | 건강한 사람이 운동 중 도달 가능한 최대 심근산소요구량 |
| 🔹 심장질환자의 협심증 발현 RPP | 10,000 ~ 25,000 | 이 수치에서 흉통, ST분절 변화 등 발생 가능 |
🧠 임상에서 어떻게 활용하냐면?
- 환자가 운동 중 협심증 발생한 RPP 지점을 기록
- 다음 운동은 그 지점의 90% 이하로 설정 (보통 80 ~ 90%)
- 예: 협심증 발현 RPP가 26,000이면 → 운동 시 목표 RPP < 23,400
🐾 기억 꿀팁 비유
💥 RPP는 심장의 연료 게이지
건강한 심장은 RPP 40,000까지도 버틸 수 있지만,
아픈 심장은 RPP 20,000만 넘겨도 경고등이 켜지는 거다냥!
그래서 “최대 RPP의 정상범위는 25,000~40,000”이라고 기억하면 돼 😽
이 문제는 개씹쓰압이 될 것임. 왜냐면 통계적 정의로 봤을 땐, 1번이 맞을 수 있기 때문임. 하지만 여기서 출제의 논점은 아마도 가장 정적편포와 이상적인 구조를 갖는 것은? 이 되어서 정답이 4번만 가능하게 됨 ㅡㅡ
이건 통계 기초 개념인 **분포의 형태(Skewness)**와
**평균(Mean), 중앙값(Median), 최빈값(Mode)**의 관계를 묻는 문제야!
정답: ✅ 4번 (C반 – ③자료)
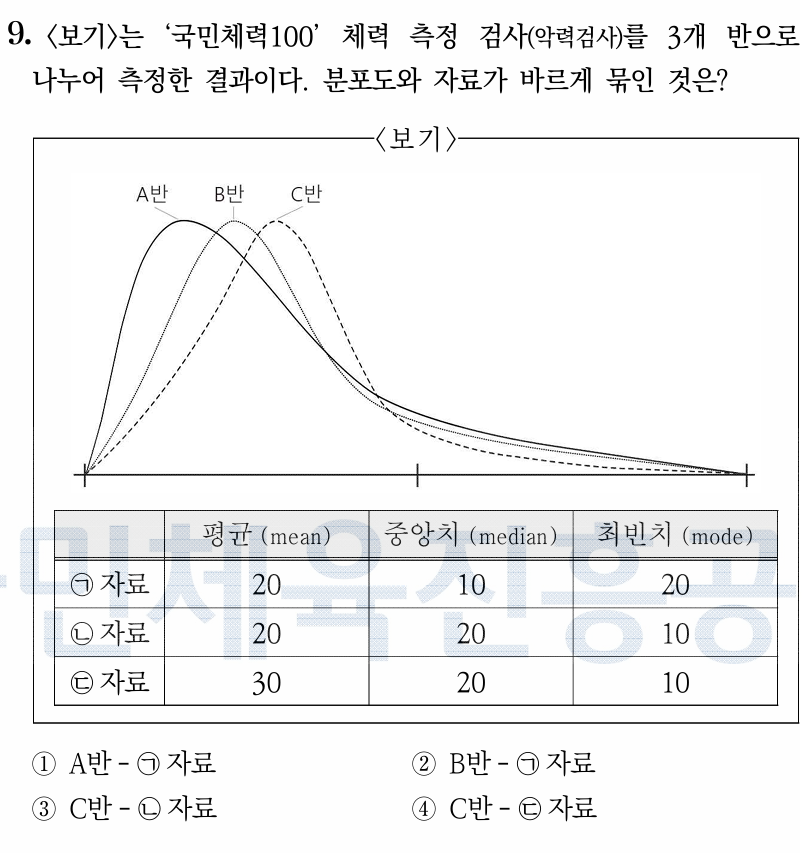
🔍 문제 이해 포인트
그래프에는 세 개의 분포 곡선이 있어:
- A반: 왼쪽으로 치우쳐 있음 (→ 왼쪽 치우침 = 오른쪽 꼬리 = Positive skew)
- B반: 종 모양 (→ 정규분포)
- C반: 오른쪽으로 치우쳐 있음 (→ 왼쪽 꼬리 = Negative skew)
📘 통계 분포 형태와 중심 경향성의 관계
| 분포 형태 | 최빈값 > 중앙값 > 평균 | 평균 > 중앙값 > 최빈값 | 평균 = 중앙값 = 최빈값 |
| 🟣 왼쪽 꼬리 (Negative skew) | ✅ | ❌ | ❌ |
| 🔴 오른쪽 꼬리 (Positive skew) | ❌ | ✅ | ❌ |
| 🟢 정규분포 (대칭형) | ❌ | ❌ | ✅ |
📊 자료별 중심경향 비교
| 자료 | 평균 | 중앙값 | 최빈값 | 해석 |
| ㄱ. 자료 | 20 | 10 | 20 | 평균 > 중앙값 → 오른쪽 꼬리 (Positive skew) → A반에 해당 |
| ㄴ. 자료 | 20 | 20 | 10 | 평균 = 중앙값 → 대칭 분포 → B반에 해당 |
| ㄷ. 자료 | 30 | 20 | 10 | 평균 > 중앙값 > 최빈값 → 왼쪽 꼬리 (Negative skew) → C반에 해당 ✅ |
✅ 정답
C반은 왼쪽 꼬리 (Negative skew) →
평균 > 중앙값 > 최빈값 구조 →
👉 ㄷ. 자료가 정답 → 정답: ④
🐾 한 줄 요약
평균, 중앙값, 최빈값 순서만 잘 기억하면 분포 형태를 정확히 읽을 수 있다냥!
오른쪽 꼬리 = 평균이 가장 크다 / 왼쪽 꼬리 = 평균이 가장 작다 기억하자!
통계 짜증난다
✅ '꼬리'는 뭐냐면?
📊 분포곡선의 끝부분에 있는 '드물게 나오는 값들'이 길게 퍼져 있는 부분이 바로 '꼬리(tail)'야!
예를 들어서!
- 만약 어떤 반의 학생들 대부분이 20점 근처인데, 몇몇 학생이 90점 이상의 높은 점수를 받았다고 해봐.
👉 이럴 때 그래프를 그리면,
- 대부분은 왼쪽에 산 모양을 이루고
- 오른쪽 끝에 조금만 사람 있는 긴 곡선이 생기지?
✔ **그 오른쪽 끝이 바로 “오른쪽 꼬리”**인 거야!
💡 가장 쉬운 기준 정리
| 꼬리 방향 | "꼬리가 길다"는 의미 | 평균은 어디로? |
| 오른쪽 꼬리 (Positive skew) | 큰 값이 소수 존재 → 그래프가 오른쪽으로 길쭉 | 평균이 오른쪽 (제일 큼) |
| 왼쪽 꼬리 (Negative skew) | 작은 값이 소수 존재 → 그래프가 왼쪽으로 길쭉 | 평균이 왼쪽 (제일 작음) |
숫자 예시를 들면 직관적으로 ‘꼬리’가 뭔지 딱! 감이 와
그래서 지금부터 3가지 분포 형태를 각각 숫자 리스트로 보여주고,
평균, 중앙값, 최빈값이 어떻게 다르게 나타나는지 보여줄게!
✅ ① 정규분포 (대칭형 예시)
| 값 | 개수 |
| 10 | 1명 |
| 20 | 3명 |
| 30 | 1명 |
👉 대칭형이다냥! 가운데가 20이고 양쪽이 비슷해
| 개념 | 값 |
| 평균 | (10+20+20+20+30)/5 = 20 |
| 중앙값 | 3번째 값 = 20 |
| 최빈값 | 20 (가장 많이 나옴) |
✅ 평균 = 중앙값 = 최빈값 → 정규분포
✅ ② 오른쪽 꼬리 예시 (Positive skew)
| 값 | 개수 |
| 10 | 2명 |
| 15 | 1명 |
| 20 | 1명 |
| 60 | 1명 |
👉 대부분은 왼쪽에 몰려 있고, 60이라는 큰 값 하나가 오른쪽 끝에 ‘꼬리’처럼 있음!
| 개념 | 값 |
| 평균 | (10+10+15+20+60)/5 = 23 |
| 중앙값 | 3번째 값 = 15 |
| 최빈값 | 10 (2번 나옴) |
✅ 최빈값 < 중앙값 < 평균
→ 오른쪽 꼬리! 평균이 가장 오른쪽으로 끌려간다
✅ ③ 왼쪽 꼬리 예시 (Negative skew)
| 값 | 개수 |
| 5 | 1명 |
| 20 | 1명 |
| 25 | 3명 |
👉 대부분이 오른쪽(25)에 몰려 있고, 5 하나만 왼쪽으로 뾰족 튀어나감 → 왼쪽 꼬리!
| 개념 | 값 |
| 평균 | (5+20+25+25+25)/5 = 20 |
| 중앙값 | 3번째 값 = 25 |
| 최빈값 | 25 |
✅ 평균 < 중앙값 = 최빈값 → 왼쪽 꼬리! 평균이 제일 왼쪽으로 끌림
🐾 최종 요약! (너가 앞으로 쓸 수 있는 말)
| 분포 | 숫자 예시 | 구조 | 꼬리 |
| 정규 | [10,20,20,20,30] | 평균 = 중앙 = 최빈 | 대칭 |
| 오른쪽 꼬리 | [10,10,15,20,60] | 평균 > 중앙 > 최빈 | 오른쪽 꼬리 (Positive skew) |
| 왼쪽 꼬리 | [5,20,25,25,25] | 평균 < 중앙 = 최빈 | 왼쪽 꼬리 (Negative skew) |
최종 둔근해의 정리
1. 평균, 중앙값, 최빈값의 정의를 먼저 이해하고, A,B,C반의 그래프 모양을 파악해본다. 산꼭대기를 기준으로! 누가 어느쪽으로 더 길게 퍼졌는지를 보면 됨.
A반은 상대적으로 오른쪽으로 길게 퍼짐 = 오른쪽 꼬리가 길다=오른쪽 꼬리가 길다의 의미는 평균이 중앙값보다 더 크다.
B반은 상대적으로 양쪽이 동일하다. (꼭대기 기점으로 좌우를 봄).=대칭적이다=중앙값과 평균값 그리고 최빈값이 동일.
C반은 상대적으로 꼭대기를 기준으로 봤을 때 왼쪽 그래프 선이 퍼져있다=왼쪽 꼬리가 길다=중앙값보다 평균이 작다.
그래서 ㄱ,ㄴ,ㄷ 자료가 표현하는 값이 어떤 반과 동일한지를 찾음.
ㄱ자료는 중앙치보다 평균값이 크다 = 평균이 크다?=오른쪽 꼬리가 길다. = A반을 뜻함
ㄴ자료는 중앙치와 평균이 동일하다 = 대칭이다 = B반을 뜻함.
ㄷ자료는 중앙치보다 평균이 더 크다.= 평균이 크다? =오른쪽 꼬리가 길다. = 해당하는 자료가 없음.
아 그런데 C반은 또 부적편포라고 ㅡㅡ... 평균이랑 중앙값으로 보고 ㅍ ㅏㄴ단해야하하는거 아니 므ㅡ???
혹시 아는 분 있으면 ㄱ댓글좀 ...
이 문제는 일단 둔다 ㅡㅡ
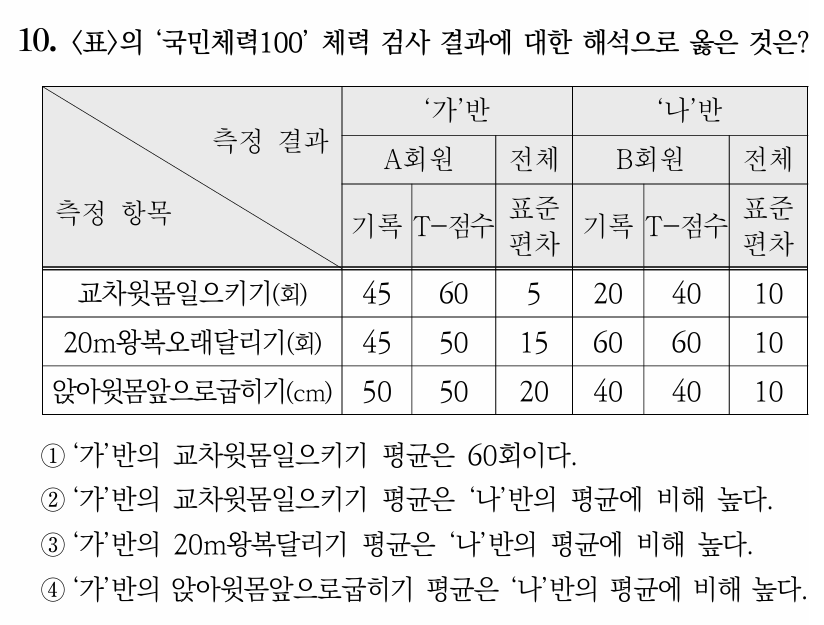
우선 평균값을 구하기 위해 T점수 공식과 Z점수 공식을 알아야 하고 한꺼번에 때려넣어서 계산할 수 있음.
🧠 T점수 공식 다시 확인

여기서:
- : T점수
- X: 개인 기록
- μ: 집단 평균
- σ: 표준편차
✅ 보기 ①
‘가’반의 교차윗몸일으키기 평균은 60회이다.
- 가반 A회원의 기록: 45회
- 가반 T점수: 60
- 표준편차: 5
우리가 구하고 싶은 건 평균 μ\mu
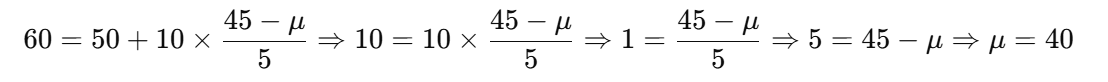
📌 정답: 평균은 40회이다.
❌ 보기에서 말한 60회는 틀림
✅ 보기 ②
‘가’반의 교차윗몸일으키기 평균은 ‘나’반의 평균에 비해 높다.
✔ 나반 계산
- B회원 기록: 20
- T점수: 40
- 표준편차: 10
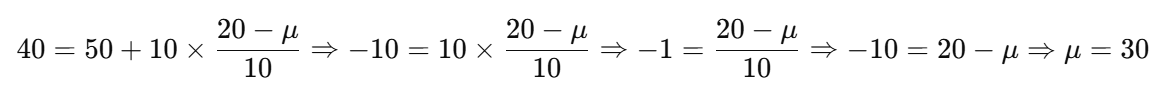
📌 가반 평균 = 40, 나반 평균 = 30
✅ 보기 맞음!
✅ 보기 ③
‘가’반의 20m왕복달리기 평균은 ‘나’반의 평균에 비해 높다.
✔ 가반 A회원 기록: 45
T점수: 50 → T점수 50 = 평균과 같은 점수
→ 평균 = 45
✔ 나반 B회원 기록: 60
T점수: 60
표준편차: 10
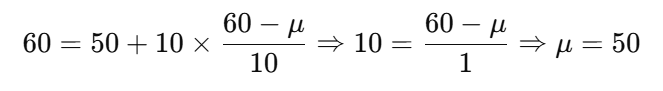
📌 가반 평균 = 45, 나반 평균 = 50
❌ 가반이 낮다 → 보기 틀림
✅ 보기 ④
‘가’반의 앉아윗몸앞으로굽히기 평균은 ‘나’반의 평균에 비해 높다.
✔ 가반 A회원 기록 = 50, T = 50 → 평균 = 50
✔ 나반 B회원 기록 = 40, T = 40, 표준편차 = 10
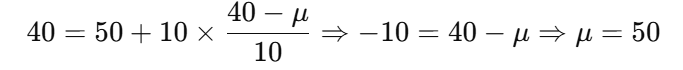
📌 둘 다 평균이 50 → 같음
❌ 따라서 보기 틀림
🎯 최종 정답: ②번
🐾 요약 정리
| 보기 | 맞음? | 이유 |
| ① | ❌ | 평균은 40인데 60이라고 잘못 말함 |
| ② | ✅ | 가반 평균 40, 나반 평균 30 → 맞음 |
| ③ | ❌ | 가반 45, 나반 50 → 보기 틀림 |
| ④ | ❌ | 둘 다 평균 50 → 보기 틀림 |
정말 귀찮고 시간 소비가 되는 문제임.
그런데 한번 풀고 나면 T점수 공식과 Z점수 공식 연습을 많이 할 수 있게 되니까 꾹 참고 풀어야함.


'📕ACSM > 23년 기출문제풀이' 카테고리의 다른 글
| 23년 건강운동관리사 운동부하검사 1-5번 기출문제 해설 및 개념정리 (1) | 2025.03.30 |
|---|---|
| 23년도 건강운동관리사 운동처방론 16-20번 기출문제 해설 및 개념정 (0) | 2025.03.30 |
| 23년 건강운동관리사 운동처방론 11번-15번 기출문제 해설 및 개념정리 (0) | 2025.03.30 |
| 23년 건강운동관리사 운동처방론 6-10번 기출문제 해설 및 개념정리 (0) | 2025.03.29 |
| 23년 건강운동관리사 운동처방론 1-5번 기출문제 해설 및 개념정 (0) | 2025.03.29 |
| 23년 건강운동관리사 건강체력평가 16-20번 기출문제 해설 및 개념정리 (0) | 2025.03.28 |
| 23년 건강운동관리사 건강체력평가 11번-15번 기출문제 해설 및 개념정리 (0) | 2025.03.28 |
| 23년 건강운동관리사 건강체력평가 1-5번 기출문제 해설 및 개념정리 (0) | 2025.03.28 |




댓글